Stasys Skėrius. Matematika Lietuvos mokslų akademijoje. Lietuvos mokslas, 1 tomas, 1993. 78-92 p.
|
Stasys Skėrus – matematikos daktaras, Matematikos ir informatikos instituto (MII) mokslinis sekretorius. 1965–1968 m. mokėsi Lietuvos mokslų akademijos Fizikos ir matematikos instituto aspirantūroje, kurią baigęs dirbo tame pačiame institute jaunesniuoju, o nuo 1974 m. vyresniuoju moksliniu bendradarbiu. 1973 m. apgynė fizikos ir matematikos mokslų kandidato disertaciją diferencialinių kooperatinių lošimų klausimais. Mokslinių interesų sritis – lošimų teorija ir kiti matematiniai operacijų tyrimo metodai. Dirbdamas Institute, skaito optimizavimo metodų, operacijų tyrimo ir lošimų teorijos kursus Vilniaus universitete, nuo 1992 m. – Vytauto Di-džiojo universitete, 1975–1979 m. yra dirbęs Orano universitete (Alžyras) dėstytoju. Kiekviename moksle yra tiek |
Nors matematika pradėta domėtis jau ir senajame Vilniaus universitete, o tarpukario metais Kauno Vytauto Didžiojo universitete susibūrė grupė labai kvalifikuotų matematikų, bet sistemingi matematikos tyrimai Lietuvoje pradėti palyginti vėlai. Pokario metais Vilniaus universitete (VU) kartu su jaunaisiais kolegomis dirbo profesoriai Petras Katilius, Vytautas Paulauskas, Zigmas Žemaitis, kurių parengti studentai, įgiję aukštesnę kvalifikaciją Rusijos mokslo centruose, pradėjo mokslinius tyrimus Lietuvoje. Antai Jonas Kubilius, baigęs Sankt Peterburgo universiteto aspirantūrą ir 1951 m. apgynęs fizikos ir matematikos mokslų kandidato disertaciją, 1952 m. ima dirbti Fizikos ir technikos institute, ką tik įkurtame Fizikos, matematikos ir astronomijos sektoriuje. Savo darbais čia J.Kubilius pradeda matematikos mokslinius tyrimus Lietuvos mokslų akademijoje. Taikydamas tikimybinius metodus skaičių teorijoje, jis per keletą metų gavo labai vertingų rezultatų, kuriuos apibendrino fizikos ir matematikos mokslų daktaro disertacijioe „Tikimybinės skaičių teorijos tyrimai“, kurią apgynė 1958 m. J. Kubiliaus monografija „Tikimybiniai metodai skaičių teorijoje“ (išleista 1959 m.) suformavo naują matematikos mokslų šaką – tikimybinę skaičių teoriją. J. Kubilius šalia mokslinio darbo dirbo ir didelį organizacinį darbą. 1956 m. spalio 1 d. įkuriamas Fizikos ir matematikos institutas. Jo pastangomis šiame institute įsteigiamas Matematikos sektorius. Jis – pirmasis šio sektoriaus vadovas, kartu ir Instituto direktoriaus pavaduotojas mokslo darbui. Aktyvus J. Kubiliaus mokslinis ir organizacinis darbas, matyt, lėmė, kad 1958 m. jis skiriamas Vilniaus universiteto rektoriumi. Dirbdamas Universitete, J. Kubilius kurį laiką dar vadovavo Instituto Matematikos sektoriui. Nuo 1959 m. šias pareigas perėmė Vytautas Statulevičius, taip pat Vilniaus universiteto auklėtinis, baigęs Sankt Peterburgo universiteto aspirantūrą pas tą patį, kaip ir J. Kubilius, vadovą akad. J. Liniką. Tačiau V. Statulevičiaus mokslo darbo kryptis kita – tikimybių teorijos ribinės teoremos. Aspirantūros metu ir baigęs ją, V. Statulevičius daug bendradarbiauja su akad. A. Kolmogorovu (Maskva), dirba pas jį. Tai, be abejo, turėjo įtakos formuojantis V. Statulevičiaus mokslo darbo krypčiai. Savo mokslų kandidato disertaciją „Nehomogeniškų Markovo grandinių lokaliosios ribinės teoremos“ (apginta 1959 m.) ir vėlesniais savo darbais V. Statulevičius pradeda kitą Vilniaus tikimybių teorijos kryptį – tikimybių teorijos ribinės teoremos. Į šiuos tyrimus įsitraukė daugelis jo mokinių. Vadovaudamas Matematikos sektoriui, V. Statulevičius rūpinosi ne tik tikimybių teorijos plėtojimu, bet ir kitų matematikos mokslo šakų – matematinės logikos, diferencialinių lygčių ir lošimų teorijos mokslinių tyrimų organizavimu. Į Rusijos mokslo centrus išvyksta Vilniaus universiteto diplomantai Vilius Matulis, Eduardas Vilkas, Bronius Grigelionis, Bronius Kvedaras, Mifodijus Sapagovas, kurie, grįžę į Lietuvą, tampa naujų matematikos tyrimo krypčių pradininkais. Apie kiekvieną iš jų, išskyrus lošimų teoriją, bus kalbama toliau. |
1967 m. V. Statulevičius išrenkamas Fizikos ir matematikos instituto direktoriumi (iki tol buvo direktoriaus pavaduotojas).
Fizikos ir matematikos institute šalia teorinės ir eksperimentinės fizikos, matematikos ir astronomijos tyrimų 6-ojo dešimtmečio pradedami kibernetikos darbai. 1962 m. Institute pradeda veikti pirmoji elektroninė skaičiavimo mašina BESM-2M, 1964 m. įsteigiamas Techninės kibernetikos sektorius (vadovas Kostas Žukauskas), o 1965 m. – Atpažinimo procesų sektorius (vadovas Laimutis Telksnys). 1977 m. sausio 1 d., antrą kartą reorganizuojant Fizikos ir matematikos institutą, įkuriami savarankiški Fizikos bei Matematikos ir kibernetikos institutai (žr. diagramą 1a pav.).
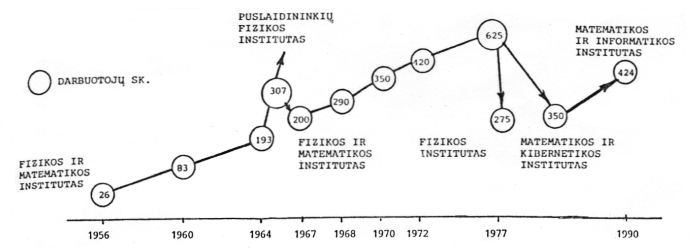 1a pav. Matematikos ir informatikos instituto raida ir darbuotojų skaičiaus kitimas.
1a pav. Matematikos ir informatikos instituto raida ir darbuotojų skaičiaus kitimas.
Matematikos ir kibernetikos institute buvo sukoncentruoti matematikos ir informatikos bei sistemotyros moksliniai tyrimai. Tuo metu, galima sakyti, jau buvo susiformavusios visos kryptys, kurios dabar yra Matematikos ir informatikos institute, tik tuometinis institutas neprilygo dabartiniam savo moksliniu potencialu (žr. diagramą 1b pav.).
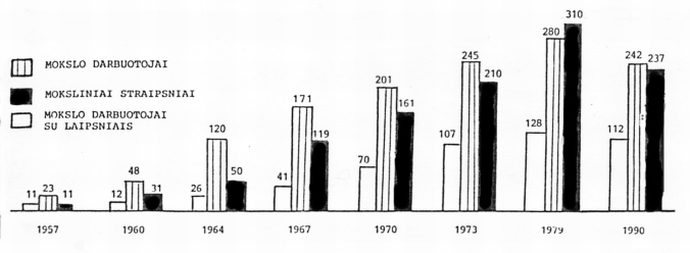 1b pav. Matematikos ir informatikos instituto darbuotojų mokslinių publikacijų dinamika.
1b pav. Matematikos ir informatikos instituto darbuotojų mokslinių publikacijų dinamika.
Antrame paveiksle nubraižytas Instituto matematikos struktūrinis medis. Susumavę šešių matematikos skyrių darbuotojų skaičių (tai matyti langelio apačioje), gauname: 83 darbuotojai, iš jų 11 habilituotų daktarų, 54 daktarai. Tai solidaus mokslinio instituto personalas. Kokį svorį turi matematikai Institute? Palyginkime gautus skaičius su 3 pav. parodytos diagramos 1993 m. skaičiais ir pamatysime, kad Instituto informatikos padaliniuose yra 6 habilituoti daktarai, o iš viso darbuotojų juose – 112, kiti 63 – aptarnaujantysis, administracinis ir ūkinis personalas. Iš bendro darbuotojų skaičiaus – matematikų mažiau negu pusė, o iš jų mokslininkų skaičius – 65%.
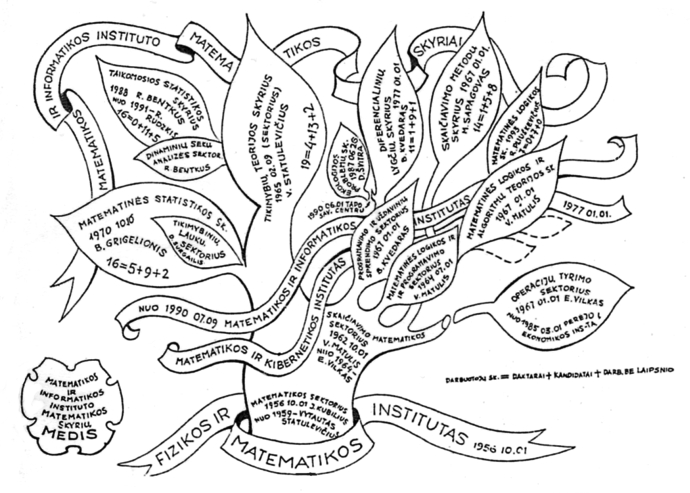 2 pav. Matematikos ir informatikos instituto matematinių skyrių medis (V. Šimkūnienės brėžinys)
2 pav. Matematikos ir informatikos instituto matematinių skyrių medis (V. Šimkūnienės brėžinys)
Dar didesnį būrį matematikų turėsime surinkę visų Lietuvos universitetų ir kitų aukštųjų mokyklų matematikos katedrų dėstytojus. Ne vienoje jų rasime Instituto aspirantūrą baigusį ir pasirinkusį profesoriaus karjerą. Iš viso Instituto (įskaitant FMI) aspirantūroje paruošta 96 mokslų kandidatai matematikai ir tik apie pusė jų dirba Institute. Daugiausia paruošė akad. V. Statulevičius – 23, akad. E. Vilkas – 12, akad. B. Grigelionis – 8 (tai be Vilniaus universiteto aspirantų).
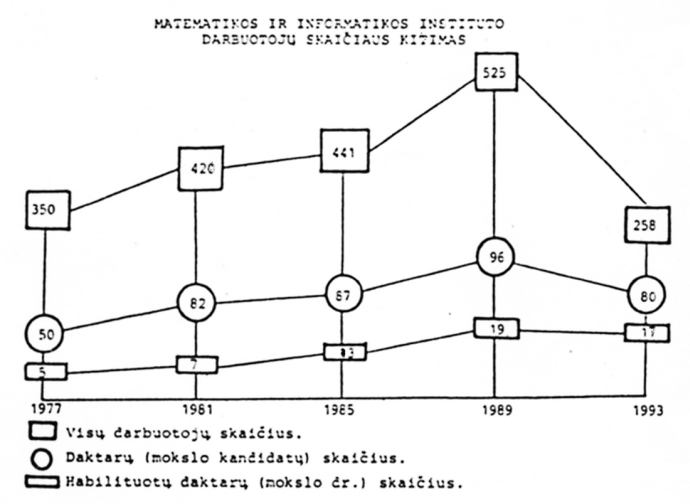 3 pav. Matematikos ir informatikos instituto darbuotojų skaičiaus ir jų kvalifikacijos kitimas (1977–1993)
3 pav. Matematikos ir informatikos instituto darbuotojų skaičiaus ir jų kvalifikacijos kitimas (1977–1993)
Nuo 1967 m. pradedamos ginti mokslų daktarų matematikų disertacijos. Per 20 metų jas apgynė 13 Institute dirbusių matematikų. Subrendus Institutui pasirodė apibendrinančių darbų, monografijų. Per pastaruosius metus parašyta ir išleista apie 10 matematikos monografijų (A. Janušauskas, V. Statulevičius ir L. Saulis, A. Tempelmanas, D. Švitra, R. Januškevičius, L. Stupelis), 3 išleistos užsienio leidyklose, už matematikos darbus buvo paskirtos 5 Lietuvos valstybinės premijos.
 1986 m. keturi Instituto darbuotojai apgynė mokslų daktaro disertacijas. Matematinės statistikos skyriaus vadovas prof. B. Grigelionis (centre) ir daktarai (iš kairės) M. Sapagovas, V. Bentkus, R. Mikulevičius, L. Saulis.
1986 m. keturi Instituto darbuotojai apgynė mokslų daktaro disertacijas. Matematinės statistikos skyriaus vadovas prof. B. Grigelionis (centre) ir daktarai (iš kairės) M. Sapagovas, V. Bentkus, R. Mikulevičius, L. Saulis.
Prieš apžvelgdamas Instituto matematikų mokslinius rezultatus, priminsiu, kad nerasime lošimų teorijos ir matematinės ekonomikos rezultatų, nes Operacijų tyrimo skyrius, vadovaujamas akad. E. Vilko, vykdęs šiuos darbus, 1985 m. kovo 1 d. buvo perkeltas į Ekonomikos institutą. Diferencialinių lygčių skyriuje išaugęs Ekologijos problemų skyrius (vadovas D. Švitra) perėjo į 1990 m. birželio 1 d. Klaipėdoje įkurtą Ekosistemų analizės centrą, o dabar priklauso Klaipėdos universitetui.
 Šiuose rūmuose Vilniuje 1985 m. įsikūrė Matematikos ir informatikos institutas.
Šiuose rūmuose Vilniuje 1985 m. įsikūrė Matematikos ir informatikos institutas.
Tikimybių teorijos ribinės teoremos
Naudojant tikimybių teorijos ar matematinės statistikos metodus įvairių realių reiškinių modeliavimui, beveik visada gaunami sudėtingi reiškiniai, užrašomi dažnai sumomis nuo nepriklausomų ar priklausomų dydžių arba integralais nuo atsitiktinių procesų ar laukų su tomis ar kitomis žinomomis charakteristikomis. O kartais tie reiškiniai yra dar sudėtingesni pradinių atsitiktinių procesų ar laukų funkcionalai, pavyzdžiui, stochastinių diferencialinių lygčių sprendiniai. Norint aprašyti šiuos reiškinius reikia žinoti jų tikimybinį pasiskirstymą. Dažnai net šiuolaikiniais kompiuteriais tų pasiskirstymų neįmanoma apskaičiuoti, be to, kad kokybiškai suprastume reiškinius, reikia jų analizinės išraiškos, kurios negauname skaičiavimais. Šiuolaikinės ribinių teoremų teorijos tikslas yra aproksimuoti šiuos sudėtingus pasiskirstymus paprastesniais, nustatyti aproksimacijos tikslumą; jeigu jis nėra pakankamas, tai norint jį pagerinti pridedama papildomų narių (asimptotiniai skleidiniai) ir pan. Ypač subtili yra labai mažų tikimybių aproksimacijos problema (lokalinės bei didelių nuokrypių teoremos).
Ribinėms teoremoms didžiulę savo darbų dalį skyrė visi tikimybių teorijos ir matematinės statistikos klasikai: P. Čebyšovas, A. Liapunovas, A. Markovas, S. Bernšteinas, A. Kolmogorovas, J. Linikas, N. Smirnovas, A. Chinčinas (Rusija), E. Borelis ir P. Levy`s (Prancūzija), H. Crameris (Krameris, Švedija), N. Wieneris ir J. Neymanas (Neimanas, JAV), A. Renyi (Vengrija). Į šiuolaikines ribinių teoremų problemas gilinasi vis daugiau mokslininkų, o pas mus ši tematika išlieka gausiausiai atstovaujama.
Kaip minėjome, V. Statulevičiaus mokslų kandidato disertacijos tema buvo „Nehomogeniškųjų Markovo grandinių lokaliosios ribinės teoremos“. Panašias teoremas buvo įrodę A. Kolmogorovas ir S. Sirašdinovas, bet tik homogeniniam atvejui: pirmasis – suvesdamas į rekurentinius ryšius, antrasis – naudodamasis charakteringų matricų spektrine teorija. Tačiai nė vienas šių metodų netinka nehomogeninei grandinei. Jau pirma V. Statulevičiaus nehomogeniniam atvejui gauta lokalinė teorema buvo 1956 m. įvertinta antrąja Leningrado (dabar Sankt Peterburgo) universiteto premija (pirmąją gavo akad. V. Fokas už knygą „Erdvės, laiko ir traukos teorija“). Tai buvo pirmas atvejis Leningrado universiteto istorijoje, kad šią premiją gautų aspirantas.
V. Statulevičius pasiūlė charakteringųjų funkcijų logaritmų išvestinių metodą, kuris ir leido išspręsti šią problemą. V. Statulevičiui grįžus į Vilnių, jo rezultatus daugiamečiam atvejui apibendrina A. Raudeliūnas (VU), stabilių ribinių dėsnių atvejui – A. Aleškevičienė. V. Statulevičius savo daktaro disertaciją paskyrė problemoms, pasitaikančioms pereinant nuo atsitiktinių dydžių nepriklausomumo prie priklausomumo, darant atsitiktinių dydžių sumų pasiskirstymų asimptotinę analizę – tiriant konvergavimo greitį, asimptotinius skleidinius, dudžiųjų nuokrypių tikimybes.
Kartu su Broniumi Riauba jis įvedė naują Markovo tipo procesų (bet ne būtinai Markovo) klasę, ir B. Riauba įrodė šiems procesams analogiškas ribines teoremas, kokios yra žinomos Markovo procesams. Pasirodė, kad ši nauja procesų klasė yra svarbi statistinei fizikai. Tirdamas atsitiktinių dydžių, susietų į sudėtingą Markovo grandinę, sumų asimptotines savybes, nemaža rezultatų (iš jų ir sustiprintą didžiųjų skaičių dėsnį) gavo G. Aleškevičius.
Norint pereiti prie priklausomų dydžių sumavimo teorijos reikėjo išspręsti keletą nepriklausomų atsitiktinių dydžių sumų problemų, kai atsitiktiniai dydžiai yra iš esmės nevienodai pasiskirstę. V. Statulevičius pirmą kartą gavo asimptotinius skleidinius Liapunovo trupmenoms, bendras sąlygas lokaliojoje teoremoje tankiams, kartu su A. Mitalausku pateikė bendriausias iki šiol žinomas sąlygas rėtiniams atsitiktiniams dydžiams lokaliojoje teoremoje. Tirdami tankių bei rėtinių atsitiktinių dydžių ribines teoremas, asimptotinius skleidinius bei konvergavimo greičius, daug nuveikė P. Survila, J. Banys, V. Pipiras (dabar jie dirba Vilniaus pedagoginiame universitete), S. Steišūnas. N. Kalinauskaitė gavo įdomių rezultatų stipriųjų ribinių teoremų srityje, analizuodama atsitiktinių dydžių sumų bei stabilų procesų trajektorijų asimptotinius dėsningumus.
Ypač daug trūkumų buvo aktualioje mažų tikimybių (vadinamųjų didžiųjų nuokrypių) teorijoje norint ją taikyti priklausomų atsitiktinių dydžių sumoms. Stigo bendrų rezultatų. Šią spragą užpildė V. Statulevičius, įrodęs bendrą didžiųjų nuokrypių lemą, kuri buvo publikuota 1966 m. žurnale „Zeitschrift fϋr Wahrscheinlichkeitstheorie und verwandte Geniete“. Vėliau L. Saulio, R .Rudzkio, V. Statulevičiaus jinai buvo apibendrinta patiems bendriausiems atvejams. Aktualus darėsi pasiskirstymų daugiamatėse ir begalinio matavimo erdvėse tyrimas. Didžiųjų nuokrypių ribines teoremas daugiamatėse erdvėse pradėjo tirti L .Vilkauskas. Vėliau spręsdamos šią problemą, daug nuveikė A. Aleškevičienė ir V. Svetulevičienė, joms pavyko įrodyti didžiųjų nuokrypių teoremas, galiojančias plačiai aibių klasei.
1967 m. V. Statulevičius apgina mokslų daktaro disertaciją „Tikimybių teorijos ribinių teoremų tyrimai“, kurioje vienas iš pagrindinių metodų yra seminvariantų metodas, V. Statulevičiui kartu su V. Petrovu (Leningrado valstybinis universitetas) ir V .Zolotarevu (V. Steklovo matematikos institutas, Maskva) paskiriama tik ką įsteigta TSRS MA Markovo premija (1971 m.). 1979 m. A. Borovkovui (Sibiro MA skyrius), V. Sazonovui (V. Steklovo matematikos institutas) ir V. Statulevičiui paskiriama TSRS valstybinė premija už faktorizacijos, sąsūkų ir seminvariantų metodų išvystymą. Seminvariantų metodas toliau tobulinamas, parodomos vis bendresnės jo galimybės (R. Rudzkis, L. Saulis, V. Statulevičius, R. Bentkus), jis pritaikomas silpnai priklausomų atsitiktinių dydžių sumų (V. Statulevičius, D. Jakimavičius), stochastinių integralų (A. Plikusas), polinominių Pitmeno statistikų (A. Basalykas), U-statistikų (A. Aleškevičienė), polinominių formų (A. Basalykas, L. Saulis, V. Statulevičius), spektrinių tankių įvertinimų (R. Bentkus) tyrimui.
Tobulinamas priklausomų dydžių asimptotinės analizės begaliniamačiu atveju metrikų metodas (P. Gudynas), logaritminių išvestinių metodas tirti konvergavimo greičiui atsitiktinių procesų ir laukų ribinėse teoremose (V. Statulevičius, J. Sunklodas).
A. Aleškevičienė su savo mokinėmis V. Naudžiūniene, L. Griniuviene, B. Kryžiene, B. Kaminskiene atliko visišką atstatymo procesų asimptotinę analizę (čia dirbo ir V. Liutikas (Vilniaus technikos universitetas), A. Baltrūnas. Vėliau buvo intensyviai tiriami polinominių formų, kartotinių integralų, įvairių netiesinių statistikų pasiskirstymai (V. Statulevičius, R. Bentkus, A. Basalykas, A. Plikusas, L. Saulis, A. Aleškevičienė).
Plečiantis tikimybių teorijos taikymui, prisireikia vis abstraktesnių modelių. Iš pradžių buvo nagrinėjami dydžiai tiesėje, vėliau prieita prie begaliniamačių funkcionalinių erdvių ir prie dar bendresnių matematinių struktūrų.
Tirdamas pasiskirstymus grupėje, svarbių rezultatų gavo A.Grincevičius, įrodęs centrinę ribinę teoremą išsprendžiamojoje matricų grupėje ir aprašęs stabilaus dydžio traukos sritį Euklido erdvės judesių grupėje.
Visą laiką buvo aktualūs integralinės geometrijos metodai geometrinių tikimybių teorijoje. Akad. V. Prochorovo (Maskva) mokinys E. Gečiauskas ištyrė iškiliosios srities atsitiktinės stygos ilgio pasiskirstymo funkciją ir atstumo tarp dviejų atsitiktinių taškų iškiliojoje srityje pasiskirstymo funkciją.
Sparčiai kilo jaunų matematikų kvalifikacija, kūrėsi savita matematikos mokykla, vis dažniau mūsų tyrimai lygiavosi į priešakines pasaulio mokslo pozicijas. 6–7 dešimtmetyje viso pasaulio įžymiausieji tikimybių teorijos ir matematinės statistikos specialistai rinkdavosi į Berklio simpoziumus. Nuo 1973 m. garsiuosius Berklio simpoziumus pakeičia Vilniaus tarptautinės tikimybių teorijos ir matematinės statistikos konferencijas. Vilnius tampa žymiausio tikimybininkų forumo vieta. Konferencija organizuojama kas 4 metai. Įvyko penkios konferencijos, šeštoji organizuojama šiemet. Į Vilnių iš užsienio mokslo centrų visada suvažiuoja daug svečių, norinčių daryti čia pranešimus, padirbėti, pabendrauti su kolegomis. Vilniaus tikimybininkai kviečiami pranešėjais į tarptautinius forumus.
Daktaro disertaciją apgina Aldona Aleškevičienė tema „Nepriklausomų atsitiktinių dydžių sumų maksimumų ir atstatymo procesų ribinės teoremos“; joje panaudojant tiesioginius tikimybinius ir analizės metodus išsprendžiama atsitiktinių dydžių sumų maksimumų bei minimumų pasiskirstymų asimptotinės analizės problema, keletas atstatymo teorijos ir atsitiktinio klaidžiojimo teisėje uždavinių. Vėliau A. Aleškevičienė tiria procesų lokalius laukus, įvairių statistikų pasiskirstymų asimptotines savybes.
Leonas Saulis 1986 m. apgina daktaro disertaciją „Aproksimavimas normaliuoju pasiskirstymu atsižvelgiant į didžiuosius nuokrypius“, kurioje išplėtoja seminvariantų metodą, gauna didžiųjų nuokrypių asimptotinius skleidinius ir parodo, kad šis metodas sėkmingai taikomas nagrinėjant atsitiktinių vektorių didžiųjų nuokrypių tikimybes. Ši tyrimo metodika buvo efektyviai panaudota priklausomų atsitiktinių dydžių ir netiesinių funkcionalų pasiskirstymų asimptotinėms savybėms tirti.
Vidmantas Bentkus disertacijoje „Nepriklausomų atsitiktinių Banacho erdvės elementų asimptotinė analizė“ iš esmės ištiria begaliniamačių erdvių specifiką tikimybių ribinėse teoremose. Priminsime, kad pirmąją šios srities mokslų daktaro disertaciją „Nepriklausomų atsitiktinių dydžių sumų ribinės teoremos Banacho erdvėse“ Vilniuje parašė Vyg. Paulauskas (VU), joje gauti rekordiniai konvergavimo greičio įverčiai. Vėliau V. Bentkus pirmasis gauna fundamentalius rezultatus tirdamas didžiųjų nuokrypių tikimybes Banacho erdvėse.
 Tikimybių teorijos skyriaus seminaras. 1-oje eilėje iš kairės: hab. daktarai A. Tempelmanas, A. Aleškevičienė, V. Bentkus, V. StatulevičiusPradėta nauja perspektyvi kryptis – kvantinės tikimybių teorijos tyrimai. Naudojant seminvariantų metodą, įrodytos centrinės ribinės teoremos (CRT) Gausso ir Poissono (Puasono) ribinių dėsnių kvantinėje tikimybių teorijoje daug bendresniems negu iki šiol nagrinėtiems atvejams (V. Statulevičius, V. Sidoravičius).
Tikimybių teorijos skyriaus seminaras. 1-oje eilėje iš kairės: hab. daktarai A. Tempelmanas, A. Aleškevičienė, V. Bentkus, V. StatulevičiusPradėta nauja perspektyvi kryptis – kvantinės tikimybių teorijos tyrimai. Naudojant seminvariantų metodą, įrodytos centrinės ribinės teoremos (CRT) Gausso ir Poissono (Puasono) ribinių dėsnių kvantinėje tikimybių teorijoje daug bendresniems negu iki šiol nagrinėtiems atvejams (V. Statulevičius, V. Sidoravičius).
Ypač vertingų rezultatų gauta pastaraisiais metais. Gauti optimalūs rezultatai greičio įverčio centrinėje ribinėje teoremoje atsitiktiniams laukams ir martingalinėje CRT.
Gauti asimptotiniai skleidiniai atsitiktinių elementų su reikšmėmis bendrose Banacho erdvėse sumų polinomams centrinėje ir lokalioje teoremose. Įrodyti asimptotiniai skleidiniai pasiskirstymo funkcijoms ir jų išvestinėms. Gauti liekanų įverčiai yra galutiniai. Rezultatai taikomi bendroms w-statistikoms.
Išspręsta daug metų egzistavusi CRT problema U ir V statistikoms. Ištirti pereinamieji reiškiniai atsitiktiniame klaidžiojime.
Įrodyta CRT Poissono proceso polinominėms transformacijoms neaprėžtos branduolinės funkcijos atveju. Įrodyta centruotų procesų polinominių formų pasiskirstymų aproksimacija kartotinių integralų Gauso matų pasiskirstymais.
Įvestos ir ištirtos integralinės metrikos tarp atsitiktinių funkcionalinių erdvių elementų, jas pasitelkus gautos aproksimacinės didžiųjų nuokrypių teoremos. Gautas eksponentinio dėsnio charakterizacijos stabilumo įvertinimas.
Išnagrinėti kai kurių trūkiųjų skirstynių skleidinių stabilumo įverčiai tolygiojoje metrikoje, vienetinio dėsnio atveju nustatyta įverčių tiksli išraiška.
Įrodytas kalibruojančių laukų Gibbso mato, konstruojamo pagal klasikinį potencialą, egzistavimas ir vienatis bei pritaikytas seminvariantų metodas nekomutuojantiems operatoriams kvantinės mechanikos centrinėje ribinėje teoremoje.
Ištirta netiesinių statistikų ir neteisiškai transformuotų Banacho erdvių elementų didžiųjų nuokrypių asimptotika. Šioms statistikoms daugiamačiu atveju gautas aproksimacijos tikslumas CRT. Įrodytos procesų su nepriklausomais pokyčiais netiesinių transformacijos ribinės teoremos ir rastos ribinių dėsnių išraiškos kaip stochastiniai integralai pagal Wienerio matą. Nustatytos sąlygos, kada k-tosios eilės politiesinės formos skirstinys konvertuoja į normaliojo dydžio Ermito polinomą, ir gautas asimptotinis skleidinys.
Nustatytos atsitiktinių sumų skirstinių konvergavimo tolygioje metrikoje būtinos ir pakankamos sąlygos. Gauta Wienerio-Hopfo lygties sprendinio aproksimacija funkcijoms, turinčioms tikimybinę prasmę.
Įrodyta didžiųjų nuokrypių teorema Poissono aproksimuojančio dėsnio atveju priklausomų atsitiktinių dydžių serijų sumoms su ψ-susimaišymu (V. Statulevičius). Išnagrinėta nepriklausomų atsitiktinių dydžių sumų skirstinio tankio didžiųjų nuokrypių asimptotinio skleidinio liekamojo nario struktūra esant Liapunovo trupmenų reguliarumo sąlygai (L. Saulis).
Buvo toliau nagrinėjami politiesinių formų skirstiniai. Įrodyta funkcionalinė centrinė ribinė teorema ir tolydinių funkcionalų iš C [0,1] nuo politiesinių formų asimptotinė teorema (A. Baslykas).
Gauta asimptotinių rezultatų dviems U-statistikų klasėms: nupjautų U-statistikų išraiškoje per paprastas U-statistikas gauti liekamųjų narių įverčiai su tikimybe 1 ir pagal tikimybę, gautos didžiųjų nuokrypių teoremos bei liekamųjų narių įverčiai funkcionalinėse ribinėse teormose (A. Aleškevičienė).
Nagrinėjamos įvairios statistikos, pavyzdžiui, w2p statistikoms įrodyti asimptotiniai skleidiniai esant labai menkoms svorių sąlygoms. Taip pat įrodytas Berry`o (Berio) – Esseeno (Eseno) įvertis daugiamatėms L-statistikoms (R. Zitikis).
Nagrinėtos kartotinių integralų pagal procesus su nepriklausomais pokyčiais asimptotinės savybės. Įrodyta centrinė ribinė teorema ir didžiųjų nuokrypių tikimybės (A. Plikusas).
Gautas optimalus konvergavimo greitis centrinėje ribinėje teoremoje m-priklausomiems atsitiktiniams dydžiams Abelio sumavimo atveju. Analogiški įverčiai gauti ir bet kokiai begalinei m-priklausomų a.d. sumai. ψ-susimaišiusiems a.d. gautos Bernsteino (Bernšteino), Bennet–Hoeffόingo (Hiofdingo), Nagajevo–Foucault`o (Fuko) tipo eksponentinės nelygybės, kuriose susimaišymo koeficientas yra daugiklis (J. Sunklodas).
Pastaraisiais metais Instituto tikimybininkai aktyviai pradeda nekomutatyvinės (arba kvantinės) tikimybių teorijos problemų tyrimą; čia dideles perspektyvas turi seminvariantų metodas. Taip V. Statulevičius ir V. Sidoravičius, naudodami seminvariantų metodą, įrodė Gausso ir Piossono dėsnių centrines ribines teoremas kvantinėje tikimybių teorijoje daug bendresniu negu iki šiol nagrinėtais atvejais. Atliekant šiuos tyrimus intensyviai bendradarbiaujama su Romos ir Paryžiaus universitetų matematikais.
Atsitiktinių procesų teorija
Pirmuosius Lietuvoje šios krypties darbus 7-ojo dešimtmečio pradžioje parašė B.Grigelionis. Vėliau šioje srityje dirbo jo mokiniai fiz. ir mat. m. daktarai Donatas Surgailis, Henrikas Pragarauskas, Remigijus Mikulevičius, fiz. ir mat. m. kandidatai Rimas Banys, Rimantas Morkvėnas, Kęstutis Kubilius, Vilniaus Universiteto matematikai fiz. ir mat. m. dr. Vygirdas Mackevičius, fiz. ir mat. m. kand. Ričardas Kudžma ir kiti.
Pirmuosiuose B. Grigelionio darbuose buvo nagrinėjami svarbūs masinio aptarnavimo ir patikimumo teorijos taškiniai procesai, kurie yra didelio skaičiaus nepriklausomųjų mažo intensyvumo taškinių procesų sumos. Pratęsęs K. Palmo (Švedija) ir A. Chinčino (Rusija) darbus, B. Grigelionis surado būtinąsias ir pakankamąsias tokių procesų silpnojo konvergavimo į Poissono procesus sąlygas bei ištyrė jų daugiamačių skirstinių asimptotinius skleidinius. Šie rezultatai yra plačiai taikomi įvairiose srityse. Vėliau šios krypties darbus tęsė R. Banys.
Sparčią atsitiktinių procesų teorijos plėtotę nulėmė 5–6 dešimtmetyje sukurtos A. Waldo (JAV) nuosekliosios analizės ir sprendžiamųjų funkcijų teorija, R. Bellmano (JAV) dinaminio programavimo koncepcija, J.L. Doobo (Dž.L. Dubo, JAV) martingalų teorija, K. Itô (Japonija) stochastinio integravimo bei stochastinių lygčių teorija ir K. Yoschidos (Japonija) ir E. Hille`o (Hilo, JAV) tiesinių sutraukiančiųjų operatorių pusgrupių teorija. Tai iš esmės pakeitė A. Kolmogorovo sukurtą Markovo procesų teoriją ir pradėjo šiuolaikinę potencialo teoriją, šiuolaikinę matematinę statistiką ir atsitiktinių procesų optimaliojo valdymo teoriją.
1968 m., remdamasis P.A. Meyerio (Prancūzija), A. Skorochodo (Ukraina) ir japonų matematikų H. Kunitos, M. Motoo, S. Vatanabės martingalų teorijos, stochastinio integravimo bei Markovo procesų teorijos darbais, B. Grigelionis įvedė lokaliai be galo dalių procesų bei jų lokaliųjų charakteristikų sąvokas, surado atsitiktinių procesų bei jų lokaliųjų charakteristikų sąvokas, surado atsitiktinių procesų su nepriklausomaisiais pokyčiais martingalinę charakterizaciją ir iš dalies sąlygas, kai lokaliai be galo dalus procesas yra stochastinės Itô lygties sprendinys. Galutinai tos sąlygos buvo ištirtos 1971 m. B. Grigelionio ir D. Surgailio darbuose. Pirmą kartą buvo įvestos ir panaudotos taškinio mato, suderinto su apibrėžta σ-algebrų šeima, ir jo kompensatoriaus sąvokos, apibendrinančios Markovo procesų trūkių mato ir Levy`o sistemos sąvokas. Vėliau buvo gauta sąlygiškai Poissono taškinių matų bei procesų su sąlygiškai nepriklausomais pokyčiais martingalinė charakterizacija.
Naudojant tikimybinių matų martingalinę charakterizaciją bei efektyvius markoviškumo kriterijus, gauti bendrieji tikimybinių matų absoliučiojo tolydumo kriterijai ir Radono–Nycodimo (Nykodimo) išvestinių formulės, kurios savo ruožtu buvo pritaikytos atsitiktinių procesų statistikoje ir informacijos teorijoje. Taip pat buvo gauta lokaliai be galo dalių procesų funkcionalų išraiška stochastiniais integralais ir, išplečiant M. Fujisakio (Fudžisakio, Japonija), G. Kalianpuro (Indija) ir H. Kunitos įdėjas, kartu gautos bendrosios netiesinės filtracijos stochastinės lygtys. Šias lygtis kitu būdu Markovo procesų netiesinei filtracijai gavo D. Surgailis.
R. Morkvėnas apibendrino D. Stroocko (Struko) ir S.R.S. Narathano (JAV) bei I. Gichmano (Rusija) darbus trūkiesiems ribiniams procesams, pasinaudojęs T. Komatsu (Komacaus, Japonija) gauta tokių procesų charakterizacija.
B. Grigelionio ir R. Mikulevičiaus sukurta tikimybinių matų silpnojo konvergavimo tipologinėse erdvėse bendroji teorija pagrįsta ribinių taškų martingaline charakterizacija. Ji apima semimartingalų ir taškinių matų silpnąjį konvergavimą, tikimybinės skaičių teorijos funkcines ribines teoremas, matematinės statistikos invariantiškumo principus, difuzinės aproksimacijos masinio aptarnavimo teorijoje, atsitiktinių procesų su reikšmėmis išsišakojusiose daugdarose silpnąjį konvergavimą bei semimartingalų su reikšmėmis Hilberto erdvėse silpnąjį konvergavimą į stochastinių evoliucinių lygčių sprendinius.
R. Mikulevičius sukonstravo atsitiktinius procesus išsišakojusiose glodžiose daugdarose su bendruoju pralaidžiu kraštu, ištyrė jų vienaties sąlygas bei Markovo savybę. Kartu buvo apibendrinta atsitiktinių procesų glodžiose daugdarose su kraštu, tenkinančių bendrąsias Felerio-Ventcelio tipo kraštines sąlygas, teorija. Į vientisą teoriją buvo sujungti žinomi D. Stroocko, S.R.S. Naradhano, S. Vatanabės, S. Nakao (Japonija), N. Portenkos, A. Skorochodo (Ukraina), S. Anulovos (Rusija) ir kitų rezultatai. Šie rezultatai apibendrinti R. Mikulevičiaus daktaro disertacijoje „Apie martingalų problemos sprendimus“, apgintoje 1986 m. Vilniuje.
Paskutiniais metais R. Mikulevičius ir H. Pragarauskas, naudodamiesi pseudodiferencialinių operatorių teorijos metodais, nustatė stochastinių diferencialinių lygčių silpnųjų sprendinių egzistavimo ir vienaties sąlygas. Šie rezultatai apibendrino ir patikslino daugelį ankstesniųjų D. Stroocko (JAV) bei japonų matematikų T. Komatsu, A. Negoro ir M. Tsuchiya (Cucijos) rezultatų.
Nagrinėdami atsitiktinių procesų sąlyginių skirstinių tankių egzistavimo ir glodumo sąlygas, B. Grigelionis ir R. Mikulevičius ištyrė parabolinio tipo stochastinių evoliucinių lygčių stipriųjų ir silpnųjų sprendinių egzistavimo, vienaties ir stabilumo sąlygas. Buvo panaudotos ir išplėstos rusų matematikų N. Krylovo ir L. Rosovskio, I. Gyongy`o (Diondžio, Vengrija), prancūzų matematikų J. Jacod`o (Ž.Žakodo), J. Memino (Ž.Memeno), E .Pardoux`o (Pardu) ir kitų ankstesniųjų darbų idėjos.
Atsitiktinių procesų optimaliojo valdymo tyrimai Lietuvos mokslų akademijoje pradėti 8-ojo dešimtmečio pradžioje H .Pragarausko darbais. Svarbiausios šios teorijos problemos yra vertės funkcijos ir optimalių arba joms artimų strategijų suradimas. Daugeliu atvejų vertės funkcijos yra Bellmano lygčių sprendiniai. Priklausomai nuo valdomųjų procesų struktūros, šios lygtys yra netiesinės skirtuminės, diferencialinės, integralinės ar integralinės diferencialinės. Žinant jų sprendinių savybes, dažnai pavyksta apskaičiuoti ir optimalias ar joms artimas strategijas.
H. Pragarausko darbuose, bendradarbiaujant su N. Krylovu, sukurta difuzijos šuolių bei šuolių procesų Euklido erdvėje ir jos sluoksniuose optimaliojo valdymo teorija. Tikimybiniais metodais ištirtos singuliariosios integralinės diferencialinės Bellmano lygtys ir jų laisvojo krašto uždavinai, pagrįsti artutiniai jų sprendimo metodai. Šie rezultatai apibendrinti H. Pragarausko daktaro disertacijoje „Stochastinių integralinių lygčių sprendinių optimaliojo valdymo teorijos klausimai“, apgintoje 1984 m. Vilniuje.
Pastaraisiais metais R. Mikulevičiaus ir H. Pragarausko darbuose tikimybiniais ir integralinių diferencialinių lygčių teorijos metodais ištirti integralinių diferencialinių Bellmano lygčių kraštiniai uždaviniai bei nustatytos bendrosios optimaliųjų strategijų egzistavimo sąlygos, ištirta išsigimusių difuzinių šuolių procesų silpna vienatis ir netiesinių intrgrodiferencialinių lygčių kraštinių uždavinių klasikinis išsprendžiamumas. Šioje srityje dirbo Arūnas Baltėnas, apibendrinęs H.J. Kushnerio (Kušnerio) algoritmus, pagrįstus atsitiktinių procesų silpnojo konvergavimo idėjomis.
Pastaraisiais metais B. Grigelionis surado bendruosius tikimybinių matų sekų kontigualumo kriterijus, apibrėžė Helingerio matų sąvoką ir juos aprašė Feynmano-Kaco tipo formule. Jis įrodė rizikos procesų atsitiktinėje Markovo aplinkoje vienpuses ir dvipuses Lundbergo nelygybes. B. Grigelionis nustatė būtinas ir pakankamas aritmetinių procesų, sukonstruotų pagal J.Kubiliaus tipo adityviasias aritmetines funkcijas su reikšmėmis Hilberto erdvėje, silpno konvergavimo prie stochastiškai tolydžių procesų su nepriklausomais pokyčiais sąlygas.
K. Kubilius gavo semimartingalų sekos funkcionalo konvergavimo prie atitinkamo specialaus pavidalo difuzinio proceso funkcionalo greičio įvertį Lévy–Prochorovo metrikoje ir nustatė difuzinio proceso atspindžiu aproksimacijos konvergavimo greičio priklausomybę nuo koeficientų glodumo.
Fiz. ir mat. m. kand. Nijolė Kalinauskaitė tyrė atsitiktinių procesų su nepriklausomaisiais pokyčiais viršutines ir apatines funkcijas, sferiškai simetriškų stabiliųjų procesų pasiskirstymo tankių skleidinius. A. Tempelmano bei fiz.ir mat. m. kandidatų Elvyros Senkienės ir Remigijaus Gylio darbuose tiesiniais metodais buvo tyriami atsitiktiniai procesai Hilberto erdvėje. A. Tempelmanas ištyrė Gaausso–Markovo procesų matų absoliučiojo tolydumo ir singuliarumo sąlygas, fiz.ir mat. m. kand. Albertas Žalys surado tokių procesų konvergavimo pagal tikimybę sąlygas.
Atsitiktinių laukų teorija
Dar 1941 m. A. Kolmogorovas aprašė visus automodeliuosius Gausso procesus. 1962 m. J. Lamperti (JAV) pastebėjo, jog visi galimi stacionariųjų sekų sumų ribiniai dėsniai sudaro automodeliųjų dėsnių klasę. Kita vertus, automodelumo sąvoka išsikristalizavo statistinėje fizikoje – fazinių virsmų renormalizacijos grupės teorijoje. 8-ame dešimtmetyje daugelis matematikų ėmė tirti automodeliuosius procesus ir laukus, jų traukos sritis ir ryšius su statistinės fizikos uždaviniais. D. Surgailio, V .Bentkaus ir fiz. ir mat. m. kandidatų Arvydo Astrausko ir Liudo Giraičio darbuose sukonstruota ir ištirta nauja automodeliųjų procesų ir laukų klasė, aprašoma stochastiniais integralais pagal Poissono matą, išnagrinėtas Gausso ir slenkančiojo vidurkio procesų funkcionalų konvergavimas į automodeliuosius procesus, įvesta funkcijos Apelio rango sąvoka ir atskleistas jos vaidmuo minėtose ribinėse teoremose. Dalis šių rezultatų buvo apibendrinta D. Surgailio daktaro disertacijoje „Tiesiniai ir jiems pavaldūs atsitiktiniai laukai“, apgintoje 1981 m. Vilniuje. Kai kuriuos iš jų beveik tuo pačiu metu gavo P. Breneris ir P. Majoras (Vengrija) bei G. Maruyana ir M. Maejima (Majedžima, Japonija). Vėliau V. Bentkaus ir D. Surgailio darbus pratęsė M. Taqqu ir Wolpertas (JAV) bei V. Verwaatas (Belgija).
Fiz. ir mat. m. kand. Elmundas Žalys kartu su P. Blecheriu (Rusija) nagrinėjo klasikinių statistinės fizikos modelių asimptotines savybes. Naudojant renormalizacijos grupės metodus ištirtas fazinių virsmų egzistavimas žinomuosiuose Dysono (Taisono) ir Migdalo modeliuose, taip pat išnagrinėti „spinų“ modeliai hierarchinėse gardelėse. Pastaraisiais metais šios gardelės susilaukė didelio fizikų ir matematikų dėmesio, nes jose apibrėžtus klasikinius modelius galima tiksliai išspręsti naudojant ESM.
8-ame dešimtmetyje, išplėtojus funkcinį integravimą kvantinėje mechanikoje ir lauko teorijoje (daugiausia JAV mokslininkų darbais), labai susidomėta Markovo laukais (Markovo laukai yra atsitiktiniai paviršiai, charakterizuojami klasikine Markovo tipo priklausomybe). Svarbių rezultatų šioje srityje gavo D. Surgailis kartu su estų matematiku T. Ataku, sukonstravę ir ištyrę naują poligoinių Markovo laukų klasę.
R. Morkvėno darbuose tiriami martingaliniai laukai plokštumoje.
A. Tempelmano darbuose daug dėmesio skiriama statistinės ergodinės Neymano ir individualiosios ergodinės Birkhoffo teoremų, svarbių statistinėje mechanikoje ir matematinėje statistikoje, apibendrinimams. Pirmieji šias teoremas homogeniškiesiems atsitiktiniams laukams daugiamatėse tiesinėse erdvėse, sveikareikšmėse gardelėse ir jų grupėse apibendrino JAV matematikai N. Wieneris, N. Dunfordas (Danfordas), H.R. Pittas, A.P. Calderonas (Kolderonas). A. Tempelmanas įrodė bendrą statistinę ergodinę teoremą amenabiliosiose grupėse, parodydamas, kad vadinamosios Fiolnerio aibių sekos yra statistiškai vidurkinančios. Be to, jis įrodė, kad lokaliai kompaktiškose grupėse egzistuoja universalios apibendrintos vidurkinančios kompaktiškų aibių sekos. A. Tempelmanas gavo ergodiškumo ir susimaišymo kriterijus homogeniškiesiems Gausso laukams. A. Tempelmanas ir jo mokiniai įrodė, kad koncentrinių, neapibrėžtai augančių rutulių sekos Lobačevskio erdvėje ir Lorentzo (Lorenco) grupėje yra individualiai vidurkinančios. Tai buvo pirmasis griežtas ergodinės Birkhofo teoremos analogo įrodymas Lobačevskio erdvėje ir Lorentzo grupėje. Vėliau ergodinės teoremos buvo apibendrintos jas taikant homogeniškiesiems atsitiktiniams matams grupėse.
Dalis minėtų tyrimų apibendrinta A. Tempelmano daktaro disertacijoje „Regresyviųjų įverčių konvergavimas ir pagrįstumas“, apgintoje 1975 m. Kijeve, ir jo monografijoje „Ergodinės teoremos grupėse“, išleistoje 1985 m.
Paskutiniais metais A. Astrauskas ištyrė Andersono modelio ir vidutinio lauko modelio pagrindinių būsenų asimptotines struktūras. Vidutinio lauko modelyje jis nustatė tarp pagrindinių būsenų lokalizacijos teoremų ir tiesinės evoliucijos atsitiktinėje stacionariojoję aplinkoje asimptotinio elgesio ryšį, ištyrė tokių evoliucijų susisluoksniavimo efektą ir šio efekto priklausomybę nuo modelio parametrų.
Taikomosios statistikos darbai
1970 m. Institute buvo pradėti sistemingi stacionarių procesų spektrinės analizės tyrimai.
V. Statulevičiaus aspirantas Raimondas Bentkus nagrinėjo empirinės spektrinės funkcijos normuotos paklaidos pasiskirstymo asimptotiką neaprėžtai didėjant stebėtos realizacijos ilgiui. Jam pavyko parodyti, kad Gausso proceso atveju C-tolydiniai funkcionalai silpnai konvertuoja į atitinkamus ribinio proceso funkcionalus, jeigu stacionaraus proceso spektrinis tankis integruojamas kvadratu. R. Bentkus patikslino ir apibendrino kai kuriuos U. Grenaderio ir M. Rozenblato, I. Ibragimovo, T. Malevičiaus, D.R. Brilingerio (Brilindžerio) ir kitų spektrinės funkcijos ir spektrinių vidurkių statistinius įverčius. Šie rezultatai gauti R. Bentkaus mokslų kandidato disertacijoje apgintoje 1972 m. R. Bentkus parodė, kad stacionaraus plačiąja prasme atsitiktinio proceso empirinių spektrinių vidurkių seminvariantai yra singuliariniai integralai, ir panaudojo šį faktą spektrinių įverčių asimptotiniam normalumui įrodyti. Vėliau šie rezultatai buvo apibendrinti kai kurioms stacionarių procesų daugiatiesinėms formoms.
Kadangi spektrinis tankis yra pati įdomiausia taikymams spektro charakteristika, nuo 1975 m. pradėti intensyviai tirti spektrinio tankio įverčiai. R. Bentkus ir jo vadovaujami aspirantai gavo didelių nuokrypių teoremas, eksponentines nelygybes tikimybėms, kad spektrinio tankio įverčio paklaida viršys pasirinktą dydį, ir asimptotinius pasiskirstymo skleidinius stacionarių Gausso procesų spektrinio tankio įverčiams. Kai kurie minėti rezultatai ne Gausso procesams buvo gauti ir susisteminti R.Rudzkio mokslų kandidato disertacijoje.
1980 m. buvo pradėti neparametrinių pasiskirstymo tankio statistinių įverčių analogiški tyrimai. Čia produktyviai darbavosi R. Bentkaus aspirantas A. Kazbaras, kuris šius tyrimus susistemino mokslų kandidato disertacijoje, apgintoje 1982 m.
Bendradarbiaujant su prof. I. Ibragimovu, R. Chasminskiu, M. Pinskeriu ir jų mokiniais dinaminių sekų analizės sektoriuje buvo pradėti minimakso neparametrinių statistinių įverčių tyrimai. Buvo asimptotiškai nustatyti minimakso neparametriniai spektrinio tankio ir pasiskirstymo tankio statistiniai įverčiai kai kuriais plačiai naudojamais apriorinės informacijos atvejais, kai informacija nusakoma tankio išvestinių arba tankio Fourier`s (Furjė) transformacijos gesimo greičio apribojimais. Šie tyrimai pratęsė kai kuriuos anksčiau atliktus I. Hajeko, I. Ibragimovo, R. Chasminskio, R. Farellio (JAV) ir kitų matematikų tyrimus asimptotinės matematinės statistikos srityje. V. Satatulevičiaus (jaunesniojo), A. Kazbaro ir R. Rudzkio darbuose gauti nauji įdomūs vadinamieji adaptyvūs pasiskirstymo tankio ir spektrinio tankio įverčiai, kuriems rekonstruoti nereikia labai detalios apriorinės informacijos. Parėmus akad. A. Kolmogorovui, sektoriuje pradėti ir eksperimentiniai neparametrinių įverčių tyrimai, naudojant šiam reikalui skaičiavimo mašinas.
Savo tyrimus stacionarių procesų neparametrinės statistikos srityje R. Bentkus apibendrino daktaro disertacijoje (1985 m.).
Reikšmingų rezultatų nestacionarių Gausso procesų didelių nuokrypių srityje gavo Rimas Rudzkis. Tai jis sėkmingai pritaikė spektrinio tankio įverčio maksimalaus nuokrypio pasiskirstymui tirti. R.Rudzkis sukūrė efektyvius neparametrinių statistinių įverčių supremumo pavidalą turinčių funkcionalų pasiskirstymo asimptotinės analizės metodus. Išnagrinėjo tikimybinio tankio ir spektrinio tankio neparametrinių įverčių maksimalaus nuokrypio pasiskirstymo asimptotiką.
 Taikomosios statistikos skyriaus darbuotojai. Antras iš dešinės stovi skyriaus vadovas R. BentkusFiz. ir mat. m. kand. Marius Radavičius, nagrinėdamas pasiskirstymo tankio statistinius įverčius, patekė naują asimptotinio efektyvumo formuluotę, apibendrinančią efektyvumą minimakso prasme ir efektyvumą pagal Bachadūrą. Jis įrodė apibendrintą Hajeko nelygybę, palengvinančią statistinių įverčių tyrimą. Buvo gauta statistinių pasiskirstymo tankio įverčių kvadratinės rizikos funkcijos asimptotinė riba iš apačios tam tikroje tankių klasėje ir sukonstruotas statistinis įvertis, asimptotiškai pasiekiantis šią ribą.
Taikomosios statistikos skyriaus darbuotojai. Antras iš dešinės stovi skyriaus vadovas R. BentkusFiz. ir mat. m. kand. Marius Radavičius, nagrinėdamas pasiskirstymo tankio statistinius įverčius, patekė naują asimptotinio efektyvumo formuluotę, apibendrinančią efektyvumą minimakso prasme ir efektyvumą pagal Bachadūrą. Jis įrodė apibendrintą Hajeko nelygybę, palengvinančią statistinių įverčių tyrimą. Buvo gauta statistinių pasiskirstymo tankio įverčių kvadratinės rizikos funkcijos asimptotinė riba iš apačios tam tikroje tankių klasėje ir sukonstruotas statistinis įvertis, asimptotiškai pasiekiantis šią ribą.
Nagrinėtas pasiskirstymo tankio parametro įverčių asimptotinio efektyvumo ir didelių nuokrypių teoremų sąryšis. Gautas asimptotiškai tikslus parametro įverčių didelių nuokrypių rėžis.
Nagrinėti empirinių laukų, pasitaikančių neparametrinėje statistikoje, nuokrypiai tolygiojoje metrikoje ir gauta pasiskirstymo asimptatika (R. Rudzkis).
Dinaminių sekų analizės sektoriuje, vėliau Taikomosios statistikos skyriuje buvo dirbami taikomieji darbai, konsultuojami biologai, medikai, inžinieriai statistikos taikymo klausimais, atliekami technikos, ekologijos, medicinos, geologijos, ekonomikos ūkiskaitiniai darbai. Paminėsime svarbiausius.
Buvusios TSRS Staklių mokslinio tyrimo instituto Vilniaus filialui pasiūlyti koordinacinių matavimo mašinų geometrinių ir temperatūrinių sisteminių paklaidų aproksimacijos metodai.
Elektrografijos mokslinio tyrimo institutui sukurti spausdintų, rankraščio ir grafinių dokumentų vaizdų skaitmeninių įrašų filtracijos matematiniai metodai, algoritmai ir programinė įranga.
Udmurtijos naftos ir dujų gamybiniam susivienijimui buvo sudaryti karotažo duomenų statistinio apdorojimo algoritmai ir programos.
Vykdant fundamentinius statistikos tyrimus ir sprendžiant taikomuosius uždavinius, išaugo darbštus mokslininkų kolektyvas, gerai išmanantis statistikos metodus ir išmokęs naudotis personalinių kompiuterių programine įranga. Skyriuje sukurta keletas taikomųjų programų paketų (TPP) statistiniams duomenims apdoroti personaliniais kompiuteriais:
- TPP atsitiktinių procesų spektrinėms charakteristikoms nustatyti,
- neparametrinių spektrinės analizės metodų TPP,
- pasiskirstymo tankių mišinių analizės paketas
- ir kitos taikomosios programos.
Toliau bendradarbiaujama su Lietuvos medikais. Daugiamatės statistikos metodais išnagrinėti rizikos veiksniai ir išgyvenimo rodikliai tiriant VU kardiologijos laboratorijos duomenis ir imunologijos rodikliai tiriant Onkologijos centro duomenis.
Bendradarbiaujant su Valstybės statistikos departamentu atliekamas darbas „Matematinių statistikos metodų diegimas reorganizuojant valstybės statistiką“. Jo tikslas – apibrėžti Lietuvos valstybinės statistikos naujos struktūros pagrindus.
Darbas apima kompiuterinių duomenų bazių sudarymo, informacijos gavimo principų parengimą, duomenų apdorojimą matematiniais metodais ir šių darbų programinės įrangos sudarymą.
Pertvarkyta valstybinė statistika padės Lietuvos vadovybei ir ūkiniams subjektams realiai vertinti ekonominę situaciją ir prognozuoti ateitį rinkos sąlygomis.
Diferencialinės lygtys ir jų sprendimo metodai
Pradėti diferencialinių lygčių tyrimus Institute buvo sumanyta 1961 metais. Tuometinio Matematikos sektoriaus vadovo V. Statulevičiaus rūpesčiu į Ukrainos kibernetikos instituto aspirantūrą pas prof. V. Šamanskį buvo nusiųstas M .Sapagovas, o į Voronežo universitetą pas prof. S. Kreiną – B. Kvedaras. Stažuotis V. Steklovo Matematikos instituto Leningrado skyriuje pas prof. O Ladyženskają išvyko L. Stupelis. Šie bendradarbiai ir buvo diferencialinių lygčių tyrimų pradininkai Institute.
Būdami skirtinguose mokslo centruose, jie dirbo skirtingose diferencialinių lygčių teorijos srityse. B. Kvedaras nagrinėjo paprastųjų diferencialinių lygčių kraštinius uždavinius, M. Sapagovas – elipsinių lygčių sprendimą baigtinių skirtumų metodais, o L. Stupelis – mišrius lygčių su dalinėmis išvestinėmis uždavinius. Pirmoji mokslų kandidato disertacija buvo apginta 1965 metais. Ją Kijeve apgynė M. Sapagovas. Po metų disertaciją apgynė B. Kvedaras, o 1967 m. – L. Supelis.
Diferencialinių lygčių specialistai nuo 1964 m. Institute susibūrė Matematinės logikos ir programavimo sektoriuje. Šiame sektoriuje greta teorinių tyrimų, pasitelkus ESM, buvo sprendžiami ūkiniai ekonominiai ir inžineriniai uždaviniai. Šių darbų apimtis plėtėsi, todėl į Institutą buvo priimami jauni žmonės, dažniausiai baigę Vilniaus universiteto Matematikos fakultetą. 1967 m. sausio 1 d., reorganizuojant Institutą, buvo įkurti Skaičiavimo metodų sektorius (vadovas M. Sapagovas), kuriame sukoncentruoti diferencialinių lygčių skaitmeninių metodų tyrimai, ir Programavimo ir uždavinių sprendimo sektorius (vadovas B .Kvedaras), kuriam pavesta atlikti teorinius ir taikomuosius diferencialinių lygčių tyrimus ir spręsti techninius bei ekonominius uždavinius. Nuo 1977 m. sausio 1 d., perdavus praktinių uždavinių, nesusijusių su diferencialinių lygčių taikymu, sprendimą kitiems padaliniams, pastarasis sektorius pavadintas Diferencialinių lygčių sektoriumi (nuo 1980 m. kovo 10 d. LMA institutų sektoriai pavadinti skyriais).
Jame susiformavo dvi teorinių tyrimų kryptys: diferencialinių lygčių teorija funkcionalinėse erdvėse, čia įskiriant ir elipsinių lygčių teoriją, ir matematinė skysčių tekėjimo teorija. Vėliau atsirado dar viena kryptis – matematinių biologijos, medicinos ir ekologijos modelių, aprašomų diferencialinėmis lygtimis, tyrimas.
Visose šiose kryptyse gauta daug fundamentalių rezultatų. Kai kuriuos jų čia ir paminėsime.
Buvo ištirti kraštiniai uždaviniai su netradicinėmis integralinėmis sąlygomis pirmos ir antros eilės diferencialinių lygčių sistemoms. Nustatytos tų uždavinių išsprendžiamumo sąlygos ir sprendinio vienaties klausimai. Sukonstruota Greeno (Grino) funkcija, kuria išreiškiami uždavinio sprendiniai (B. Kvedaras). Gautieji rezultatai leido minėtų uždavinių tyrimams pritaikyti klasikinę kraštinių uždavinių teoriją. Pasiūlytas apibendrintosios Greeno funkcijos sudarymo diferencialinio operatoriaus spektro taške metodas (fiz. ir mat. m. kand. J. Macionis). Remiantis šia funkcija ištirta plati diferencialinių operatorių spektro perturbavimo uždavinių klasė ir sudaryti algoritmai perturbuotų tikrinių reikšmių ir tikrinių funkcijų apskaičiavimui (B. Kvedaras). Jie pritaikomi teorinėje fizikoje nagrinėjant kai kurias Schrödingerio (Šrėdingerio) operatoriaus modifikacijas. Nustatytos pakankamos, atskirais atvejais ir būtinos, sprendinio egzistavimo sąlygos diferencialinei lygčiai Banacho erdvėje su išsigimusiu operatoriumi prie išvestinės. Nustatyta šių lygčių sprendinių struktūra ir išspręsti kai kurie kraštiniai uždaviniai (J. Macionis).
Panaudojus Diferencialinių lygčių skyriuje sukurtą metodiką, išnagrinėtos silpnai išsigimstančios pirmos eilės diferencialinės lygtys Banacho erdvėje. Šių tyrimų rezultatai leido Fukso teoriją, sukurtą paprastoms diferencialinėms lygtims su analiziniais koeficientais, pritaikyti diferencialinėms lygtims Banacho erdvėse su operatoriais analitiškai priklausančiais nuo argumento.
 Diferencialinių lygčių skyriaus vadovas mat. dr. B. Kvedaras (pirmas iš kairės su kolegomis mat. daktarais A. Grigelioniu, J. Macioniu, O. Dulkyte, S. RutkauskuBene brandžiausi rezultatai buvo gauti tiriant išsigimstančias elpsines lygtis. Kai lygtis išsigimsta arba nėra griežtai elipsinė, atsiranda efektai, kurie neleidžia jų tyrimui taikyti žinomų metodų. Tokių lygčių tyrimai pradėti 1951 m., pasirodžius M. Kieldyšo darbams. Fiz. ir mat. m. kandatai D. Jurgaitis, B. Kvedaras, S. Rutkauskas ištyrė stipriai išsigimstančių hiperplokštumoje elipsinių lygčių ir sistemų sprendinių struktūrą, asimptotines savybes, sudarė metodiką sprendinio asimptotinio skleidinio nariams apskaičiuoti. Jie ištyrė keletą neklasikinių kraštinių uždavinių ir nustatė sąlygas, kada klasikiniai uždaviniai nėra korektiški arba neišsprendžiami; ištyrė plačias korektiškų neklasikinių uždavinių klases, jų išsprendžiamumo bei sprendinio vienaties sąlygas, sprendinių asimptotiką ir kitas savybes. E. Paliokas išnagrinėjo silpnai susijusias su Cauchi`o (Koši)-Riemanno (Rimano) daugiamečiais analogais elipsinių lygčių sistemas ir nustatė Dirichlet`o (Dirichlė) uždavinio išsprendžiamumo priklausimą nuo sistemos koeficientų įvairiose puserdvėse ir begaliniame sluoksnyje. Gautieji rezultatai yra svarbus indėlis į šiuo metu smarkiai besivystančią išsigimstančių elipsinių lygčių analizinę teoriją bei šių lygčių kraštinių uždavinių teoriją.
Diferencialinių lygčių skyriaus vadovas mat. dr. B. Kvedaras (pirmas iš kairės su kolegomis mat. daktarais A. Grigelioniu, J. Macioniu, O. Dulkyte, S. RutkauskuBene brandžiausi rezultatai buvo gauti tiriant išsigimstančias elpsines lygtis. Kai lygtis išsigimsta arba nėra griežtai elipsinė, atsiranda efektai, kurie neleidžia jų tyrimui taikyti žinomų metodų. Tokių lygčių tyrimai pradėti 1951 m., pasirodžius M. Kieldyšo darbams. Fiz. ir mat. m. kandatai D. Jurgaitis, B. Kvedaras, S. Rutkauskas ištyrė stipriai išsigimstančių hiperplokštumoje elipsinių lygčių ir sistemų sprendinių struktūrą, asimptotines savybes, sudarė metodiką sprendinio asimptotinio skleidinio nariams apskaičiuoti. Jie ištyrė keletą neklasikinių kraštinių uždavinių ir nustatė sąlygas, kada klasikiniai uždaviniai nėra korektiški arba neišsprendžiami; ištyrė plačias korektiškų neklasikinių uždavinių klases, jų išsprendžiamumo bei sprendinio vienaties sąlygas, sprendinių asimptotiką ir kitas savybes. E. Paliokas išnagrinėjo silpnai susijusias su Cauchi`o (Koši)-Riemanno (Rimano) daugiamečiais analogais elipsinių lygčių sistemas ir nustatė Dirichlet`o (Dirichlė) uždavinio išsprendžiamumo priklausimą nuo sistemos koeficientų įvairiose puserdvėse ir begaliniame sluoksnyje. Gautieji rezultatai yra svarbus indėlis į šiuo metu smarkiai besivystančią išsigimstančių elipsinių lygčių analizinę teoriją bei šių lygčių kraštinių uždavinių teoriją.
L. Stupelis nagrinėjo antros eilės diferencialines lygtis su dalinėmis išvestinėmis srityse, kuriose keičiasi lygties tipas. Ištyrė, kada pradiniai ir kraštiniai uždaviniai yra korektiški, nustatė sprendinių egzistenciją ir vienatį bei kokybines savybes. Vėliau pradėjo nagrinėti stacionarių skysčių tekėjimą inde su laisvu paviršiumi, aprašomu Maxwellio (Maksvelio) lygčių sistema. Esant mažam Reynoldso (Reinoldso) skaičiui, jis įrodė sprendinių egzistenciją ir vienatį svorinėse erdvėse ir gavo laisvo paviršiaus išraišką. Išnagrinėjo keletą modelinių uždavinių įvairiose funkcionalinėse erdvėse, nustatė apriorinius sprendinių įverčius. Kraštinius uždavinius begalinėse juostose ir kai kuriose elementariose srityse su nuliniais kampais Navier`o (Navje)–Stokeso (Stokso) ir Maxwellio lygčių sistemoms ištyrė K. Samaitis.
Labai vertingų rezultatų tirdamas Navier`o-Stokeso sistemos kraštinius uždavinius begalinėse srityse su laisvu paviršiumi, gavo K. Pileckas. Jisai pirmasis surado laisvo paviršiaus asimptotiką begalybėje ir sprendinių priklausomybę nuo jos. Ištyrė solenoidinių vektorių laukų erdvių savybes ir nustatė, kada sprendiniai yra šių erdvių elementai. Išsprendė keletą uždavinių, kuriuose nagrinėjo klampaus nesuspaudžiamo skysčio judėjimą srityje, turinčioje dvi begalines atšakas ir laisvą paviršių. A. Grigelionis nustatė variacinių stangrumo skaičiavimo uždavinių, sąlyginio ir absoliutaus ekstremumo egzistavimo sąlygas, kai duota sritis su laisvu kontūru.
Fiz. ir mat. m. dr. Donatas Švitra (dabar dirba Klaipėdos universitete) nagrinėjo netiesines diferencialines lygtis su vėluojančiu argumentu, kai vėlavimas priklauso nuo ieškomos funkcijos. Labai detaliai ištyrė bifurkacijos uždavinių savybes, ypač jų kvazipolinomų šaknų savybes. Vėliau D. Švitra pradėjo tirti biologijos ir medicinos matematinius modelius, aprašomus diferencialinių lygčių su vėluojančiu argumentu sistemomis. Jis ir jo vadovaujami bendradarbiai (A. Grikienis, R. Jančiauskas, R. Laugalys, J. Valančius) sukūrė ir išnagrinėjo kraujo gamybos procesų matematinius modelius, skydliaukės funkcionavimo matematinę teoriją, gliukomijos matematinio modeliavio ir insulino reguliavimo kraujyje klausimus, vabzdžių laboratorinės populiacijos matematinį modelį ir kitus uždavinius.
Fiz. ir mat. m. kand. Ona Dulkytė dirbo diferencialinių lygčių taikymo srityje. Ji sudarė programinę sistemą geofiltraciniams parametrams skaičiuoti pagal bendruosius išpumpavimus; ta sistema naudojama įvertinant požeminio vandens eksploatacines atsargas, ruošiant naujas vandenvietes Vilniuje, Tiumenėje, Minske, Maskvoje, Charkove ir kitur.
Dar labiau suintensyvėjo diferencialinių lygčių teorijos tyrimai grįžus iš Novosibirsko fiz. ir mat. m. dr., prof. Algimantui Janušauskui. Per pastaruosius penkis metus iš šios tematikos parašytos ir išleistos 5 monografijos (A. Janušauskas, D. Švitra, L. Stupelis).
Toliau buvo tiriami kraštiniai uždaviniai stipriai išsigimusioms elipsinėms lygtims. Hiperplokštumoje išsigimstančioms lygtims buvo ištirtas Dirichlet"o tipo kraštinis uždavinys; cilindrinio tipo srityje rastos jo išsprendžiamumo ir sprendinio vienaties sąlygos. Įrodytas maksimumo principas ir išspręstas elipsinių lygčių sistemos Dirichlet`o uždavinys srityje su ypatumu vidiniame taške.
Buvo tiriamos Navier`o–Stokso lygtys srityse su dviem išėjimais į begalybę ir laisvu paviršiumi. Joms gautos sprendinio egzistavimo ir vienaties teoremos, sprendinio bei laisvo paviršiaus asimptotika.
Ištirtas Riemanno–Hilberto kraštinių uždavinys diferencialinių lygčių sistemoms, kurios yra trimačiai ir keturmečiai Cauchy`o–Riemanno sistemos analogai. Gauti kriterijai, kai šis uždavinys yra Noetherio (Nėtario) tipo.
Ištirta keletas klampaus nesuspaudžiamo skysčio tekėjimo mdelių.
Kartu su diferencialinių lygčių teorijos tyrimais Institute buvo atliekami darbai iš šių lygčių sprendimo metodų srities. Ši tyrimų kryptis tapo pagrindine Skaičiavimo metodų skyriaus tematika nuo pat šio skyriaus įsikūrimo 1967 m.
Diferencialinėmis lygtimis aprašomi realūs fizikos, mechanikos, technikos, chemijos, biologijos reiškiniai bei procesai. Šie reiškiniai daugiausia yra netiesiniai, o atitinkančios juos netiesinės diferencialinės lygtys paprastai gali būti išsprendžiamos tik apytiksliais skaitmeniniais metodais. Tokių netiesinių elipsinio tipo diferencialinių lygčių sprendimas skirtuminiais metodais sudarė M.Sapagovo mokslų kandidato disertacijos pagrindą, o vėliau ilgą laiką buvo viena iš svarbiausių Skaičiavimo metodų skyriaus mokslinių krypčių. Nagrinėjant šių lygčių sprendimą, buvo naujai teoriškai pagrįsti apytiksliai metodai. Čia buvo remtasi monotoninių operatorių teorija. Vėliau toks netiesinių uždavinių sprendimo metodas buvo plačiai nagrinėjamas ir plėtojamas daugelio užsienio matematikų darbuose.
1973 m. apgintoje mokslų kandidato disertacijoje ir vėliau pasirodžiusiuose straipsniuose Vytautas Kleiza išnagrinėjo netiesinių uždavinių (taip pat ir elipsinų diferencialinių lygčių) sprendimo Monte Karlo metodu. Buvo įrodyta, kad šiuo metodu galima ne tik apskaičiuoti apytikslį netiesinio uždavinio sprendinį, bet ir skaitmeniškai patikrinti netiesinio uždavinio sprendinio egzistavimo vienaties kriterijų.
1967 m. pradėta tirti nauja diferencialinių lygčių klasė – diferencialinių operatorių tikrinių reikšmių uždaviniai. Buvo sukonstruoti ir teoriškai pagrįsti aukšto tikslumo skirtuminiai metodai elipsinių diferencialinių operatorių tikrinėms reikšmėms skaičiuoti. Pirmą kartą pavyko pagrįsti padidinto tikslumo skirtuminius metodus diferencialinių operatorių su kintamais koeficientais tikrinėms reikšmėms skaičiuoti. Šie teoriniai tyrimai buvo glaudžiai susiję su praktinių uždavinių sprendimu (bangolaidžių parametrų optimizavimas pagal jų savuosius virpesius). Iš šios srities Dangutė Sapagovienė 1976 m, apgynė mokslų kandidato disertaciją, kuri atitiko tuo metu naujai besiformuojančią skaičiavimo matematikos kryptį, vėliau pavadintą skaitiniu eksperimentu. Visą pastarąjį dešimtmetį skaitinis eksperimentas buvo plačiai ir sparčiai plėtojamas kaip naujas mokslinių techninių uždavinių sprendimo ir naujas įvairių mokslo šakų mokslinių tyrimų metodas.
Nuo 1972 m. po skyriaus vadovo M. Sapagovo mokslinės stažuotės Didžiosios Britanijos universitetuose Skaičiavimo metodų skyriuje pradėti padidinto tikslumo skirtuminių schemų tyrimai netiesinėms elipsinio tipo diferencialinėms lygtims. Atlikus tyrimus, buvo gauti du svarbūs rezultatai. Kvazitiesinėms elipsinio tipo diferencialinėms lygtims sukurtas iš principo naujas būdas skirtuminiams metodams parengti ir jiems pagrįsti. Silpnai netiesinėms elipsinėms lygtims buvo sudarytos ir pagrįstos susimetrintos padidinto tikslumo skirtuminės schemos. Šis rezultatas buvo apibendrintas Rimanto Skirmanto fiz. ir mat. m. kandidato disertacijoje, apgintoje 1981 metais. Joje skaitiniai sprendimo metodai buvo pradėti taikyti naujai uždavinių klasei – mikroelektronikos uždaviniams.
Nuo 1976 m. bendradarbiaujant su Kauno politechnikos instituto (KPI) mokslo tiriamuoju sektoriumi „Vibrotechnika“, Skaičiavimo metodų skyriuje imta spręsti uždavinius, susijusius su kontaktų iš skysto metalo projektavimu. Tai paskatino pradėti naujus teorinius diferencialinių lygčių su integraline sąlyga sprendimo metodų tyrimus. Ši kryptis dabar yra viena iš pagrindinių teorinių krypčių. Iš šios tematikos Raimondas Čiegis 1984 m. apgynė fiz. ir mat. m. kandidato disertaciją, kurioje išsamiai išnagrinėjo parabolinių lygčių su integralne sąlyga sprendimo metodus. Ši tematika sudarė M. Sapagovo fiz. ir mat. m. daktaro disertacijos (1986 m.) esminę dalį.
Skaitinį eksperimentą nuosekliai panaudojo netiesinės difuzijos uždaviniuose, kaip vienoje svarbiausių mikroelektronikos technologijų Vytautas Būda savo darbuose, kurie buvo apibendrinti 1986 m. apgintoje mokslų kandidato disertacijoje. Sakitinio eksperimento metodu buvo parodyta, kad tam tikromis sąlygomis neteisinės difuzijos procese gali egzistuoti neįprastas fizikos reiškinys – lokalizacijos efektas, kurį galima efektyviai panaudoti technologiniuose procesuose. Sprendžiant šį mikroelektronikos uždavinį buvo glaudžiai bendradarbiaujama su M. Keldyšo taikomosios matematikos instituto mokslininkais – akad. A. Samarskiu, nariu korespondentu S. Kurdiumovu, dr. J. Popovu (Maskva).
Teoriniams skaičiavimo matematikos tyrimams būdingas glaudus teorijos ir taikymų ryšys. Viena iš šio ryšio formų – programinės įrangos sudarymas diferencialinėms lygtims spręsti. Bendromis Skaičiavimo metodų skyriaus darbuotojų pastangomis 1979–1981 m. buvo sukurtas taikomųjų programų paketas netiesinėms elipsinėms diferencialinėms lygtims spręsti. Šis paketas, palyginti su kitais analogiškais darbais turi daug pranašumų. Jame yra speciali aukšto lygio įvedimo kalba, realizuota daugelis šiuolaikinių netiesinių diferencialinių lygčių sprendimo metodų, jis leidžia automatiškai parinkti metodą. Skyriaus darbuotojai sukūrė daugiau kaip 20 programų, sudarytų remiantis originaliais sprendimo metodais skirtais netiesinėms diferencialinėms lygtims spręsti.
1985 m. pradėta nagrinėti netiesinės lazerinės optikos uždavinių sprendimo metodus (R. Čiegis, S. Norvaišas). Gauta originalių rezultatų sprendžiant neklasikinius tamprumo teorijos uždavinius (Z. Vasiliauskas). Plačiai išnagrinėtas minimalaus paviršiaus lygčių sprendimo metodų taikymas statybinėje mechanikoje (G. Kairytė, M. Sapagovas). Sukurti nauji efektyvūs metodai magnetinio lauko potencialui skaičiuoti (T. Šeibakas). Kartu su KPI Panevėžio vakarinių fakultetu išnagrinėtas plonų metalinių sluoksnių matematinis modelis (V. Kleiza, T. Veidaitė). Nuo 1980 m. Institute kartu su Vilniaus inžinerinio statybos instituto (dabar Vilniaus technikos universitetas) Fizikos katedra nagrinėjami Baltijos jūros radioaktyvaus užterštumo nustatymo ir prognozavimo matematiniai modeliai (V. Kleiza). Sprendžiama daug kitų aktualių Lietuvos ūkio uždavinių, aprašomų diferencialinėmis lygtimis.
Pastaraisiais metais sudaryti ir pagrįsti efektyvūs skaitiniai metodai netiesinės optikos diferencialinių lygčių sistemai spręsti. Ištirtas ekonomiškų skirtuminių schemų daugiamečiams nestacionariems uždaviniams spręsti asimptotinis stabilumas (R. Čiegis).
Ištirta paprastų diferencialinių lygčių su nelokalia sąlyga sprendinio egzistencija ir sprendinių skaičius, kai netenkinama vienintelio sprendinio egzistavimo sąlyga; ištirtos skirtuminės schemos šiems uždaviniams spręsti (M. Sapagovas).
Plėtojant baigtinių skirtumų teoriją ir skaičiavimo eksperimento metodiką, įrodyti konvergavimo algoritmai difuzijos-reakcijos uždaviniams, išsigimstančių lygčių difuzijos sistemoms su netiesiniu išsigimimo koeficientu. Ištirta nauja iteracinių procesų klasė tiesinių lygčių sistemoms.
Sukonstruota ir ištirta klampių vienmačių barotropinių dujų simetriško judėjimo magnetiniame lauke skirtumų schema, įrodytas šilumai laidžių dujų entropijos nemažėjimo dėsnis.
Matematinė logika
Šios srities pradininkas Lietuvos mokslų akademijoje yra fiz. ir mat. m. kand. Viliu Matulis, apgynęs disertaciją 1964 m.
Nuo 1967 m. matematinės logikos tyrimai atliekami Matematinės logikos ir algoritmų teorijos skyriuje (iki 1993 m. vadovas V. Matulis), nuo 1993 m. – Matematinės logikos skyriuje (vadovas fiz. ir mat. m. kand. Regimantas Pliuškevičius). Pagrindinės mokslinių darbų kryptys – loginio įrodymo teorija, algoritmų sudėtingumo įvertinimas ir matematinės logikos taikymas informatikoje.
Viena esminių loginių skaičiavimų taisyklių yra struktūrinė pjūvio taisyklė, žinoma matematikams kaip išradėjo paradoksas. Jos esmė: norint įrodyti kokį nors teiginį neretai patogiau ir lengviau įrodyti stipresnį teiginį. 1935 m. G.Gentzenas (Gencenas, Vokietija) gavo fundamentalų rezultatą: jis nustatė struktūrinės pjūvio taisyklės pašalinimo galimybę iš klasikinio ir konstruktyviojo predikatų skaičiavimo. Šis rezultatas skatino ištirti kitų struktūrinių taisyklių pašalinimo galimybes. Tokį rezultatą klasikiniame predikatų skaičiavime gavo V. Matulis ir nepriklausomai nuo jo tuo pat metu žymus švedų matematikas S. Kangeris. Be to, V. Matulis įrodė, kad klasikiniame predikatų skaičiavime įrodymo paiešką galima konstruoti vieninteliu būdu, kartu apibendrindamas Wang Hao (JAV) rezultatą klasikiniame teiginių skaičiavime.
7-ojo dešimtmečio viduryje R.Pliuškevičius tyrė struktūrinių taisyklių leistinumą konstruktyviosios logikos skaičiavimuose. Kiek silpnesnius rezultatus tuo pačiu metu nepriklausomai nuo R. Pliuškevičiaus rezultatų gavo H. Curry`s (Karis, JAV). Be to, R.Pliuškevičius sukonstravo Kangerio tipo konstruktyviosios logikos taikomųjų skaičiavimų sistemą. Fiz. ir mat. m. kand. Aida Pliuškevičienė sukūrė bendrą metodą, kaip aksiominei teorijai su lygybe sukonstruoti skaičiavimą, turintį labai ribotas pjūvio tipo taisykles. Metodas buvo pritaikytas konkrečioms matematinėms teorijoms, pavyzdžiui, R. Robinsono aritmetinei sistemai buvo sukonstruotas skaičiavimas, neturintis pjūvio tipo taisyklių. Remiantis sukurtomis sekvencinėmis skaičiavimo sistemomis, buvo apibendrintas Maslovo aksiominių teorijų su lygybe atvirkštinis metodas.
1976 m. R. Pliuškevičiaus iniciatyva Institute buvo pradėti programinių (algoritminių) logikų tyrimai. Programinės logikos leidžia matematinės logikos metodais atlikti programų analizę ir sintezę, apibrėžti įvairių programavimo kalbų semantiką. Paaiškėjo, kad algoritminės logikos yra labai turiningos naujo tipo neklasikinės logikos, apimančios algoritmų teorijos ir modalinių logikų elementus. Buvo ištirti kai kurie programinių logikų įrodymo teorijos klausimai. Fiz. ir mat. m. kand. Jūratė Sakalauskaitė įrodė propozicinės dinaminės logikos (neklasikinė logika, įvesta V. Pratto (JAV) 1976 m., leidžianti patogiai aprašyti programų savybes) su begaline iteracija pilnumą, patvirtindama žinomą R. Streeto (Strito, JAV) hipotezę. Fiz. ir mat. m. kand. Kastytis Gečas pasiūlė ir pagrindė paskirstytųjų programų loginės analizės metodus, leidžiančius aprašyti ir ištirti paskirstytojo lygiagretaus programavimo kalbų semantines savybes.
1979 m. buvo pradėti algoritmų teorijos tyrimai. Fiz. ir mat. m. kand. Stasys Jukna, vadovaujamas žymaus matematiko J. Janovo (Maskva), sukūrė „patikimų“ programų ir „nepatikimų“ elementų sintezės metodus, leidžiančius asimptotiškai nedidinti programų sudėtingumo, net didėjant programų trikdžiams. Gauti asimptotiniai atitinkamų Shenono (Šenono) funkcijų įverčiai, įrodantys pasiūlytų metodų optimalumą. Vėliau S. Jukna atskleidė bendrą „entropijos išsaugojimo“ principą ir, juo remdamasis, sukūrė vienos iš pagrindinių algoritmų teorijos problem – efektyvių sudėtingumo įverčių konstravimo sprendimo metodą. Fiz. ir mat. m. kand. Valentinas Kriaučiukas, vadovaujamas A. Slisenko (Sankt Peterburgas), aprašė ir ištyrė perrinkimo uždavinių klases, kuriose efektyviai pritaikomi nekompoziciniai sprendimo metodai.
Pastaraisiais metais gauta daug įdomių matematinės logikos rezultatų. Sukurti pjūvio taisyklės eliminavimo teoremos įrodymo metodai svarbioms informatikos funkcinėms dinaminėms bei temporalinėms logikoms. Pateiktas infinitariųjų taisyklių redukcijos metodas, leidžiantis įrodyti plačios funkcijų temporalinių logikų klasės pilnumą. Išplėstas modalinių logikų indeksų metodas. Pasiūlytas dinaminių bei temporalinių logikų nedisjungčiosios rezoliucijos metodas. Sudarytos įvairių neklasikinių logokų, aprašančių algoritminių procesų savybes efektyvios aksiomų sistemos. Sukurti efektyvūs išvedimo formos įvairiose laiko logikose specializacijos metodai. Jų pagrindu sudarytas kompiuterių tinklų protokolų verifikavimo metodas.
Pasiūlytas procesų sąveikos paskirstytosiose programose formalaus loginio aprašymo metodas. Pasiūlyta ir pagrįsta paskirstytųjų procesų kompozicinė Hoare`o (Horo) tipo aksominė sistema. Buvo nagrinėjamos dinaminės logikos ir loginių programų semantikos sąsajos. Tuo pačiu metu ir nepriklausomai nuo C. Kento ir B. Hadsono (Kanada) gauta NP-pilnų aibių diofantiškoji charakterizacija. Pasiūlytas bendras „entropijos išsaugojimo“ skaičiavimo procesuose principas. Remiantis šiuo principu sukurtas bendras loginių schemų apatiniųjų sudėtingumo įverčių sudarymo metodas. Pasiūlytas naujas apatinių įverčių gavimo metodas, paremtas minimalių schemų nestabilumu. Gautas bendras universaliosios funkcijos leistinosiose aibėse egzistavimo kriterijus. Aprašytos struktūros, kuriose nėra efektyvios universaliosios funkcijos.
Kadangi MII matematikų mokslinio tyrimo rezultatai buvo pateikti palyginant su kitų šalių mokslininkų darbais, galime spręsti apie tarptautinį mūsų matematikų pripažinimą. Tai patvirtina kad ir toks dalykas: žymiausieji Instituto matematikai V. Statulevičius, B. Grigelionis, D. Surgailis, H. Pragarauskas, M. Sapagovas skaitė kviestinius pranešimus tarptautinėse konferencijose ir simpoziumuose. Akad. V. Statulevičiui vieninteliam iš Lietuvos matematikų teko garbė 1974 m. skaityti kviestinį pranešimą Pasaulio Matematikų kongrese Vankuveryje (Kanada).
 1993 m. birželio 28-liepos 3 d. Vilniuje įvyko 6-oji Tarptautinė Vilniuas tikimybių teorijos ir matematinės statistikos konferencija – stambiausiais pasaulio šios šakos forumas. Jis, 1977 m. iš Berklio (JAV, Kalifornija) persikėlęs į Vilnių, vyksta kas ketveri metai. Šiemet joje dalyvavo 180 užsienio šalių ir daugiau kaip 50 Lietuvos matematikų. Konferencijos dalyvius pasveikino Lietuvos prezidentas A. Brazauskas. Plenariniame posėdyje buvo išklausyti 2 pranešimai: Sietlo (JAV) universiteto prof. J.A. Wellneris nagrinėjo statistikos, o Romos universiteto Volteros matematikos centro prof. L. Accardis – kvantinės tikimybių teorijos problemas. Dirbta 6 sekcijose, perskaityta 216 216 pranešimų.
1993 m. birželio 28-liepos 3 d. Vilniuje įvyko 6-oji Tarptautinė Vilniuas tikimybių teorijos ir matematinės statistikos konferencija – stambiausiais pasaulio šios šakos forumas. Jis, 1977 m. iš Berklio (JAV, Kalifornija) persikėlęs į Vilnių, vyksta kas ketveri metai. Šiemet joje dalyvavo 180 užsienio šalių ir daugiau kaip 50 Lietuvos matematikų. Konferencijos dalyvius pasveikino Lietuvos prezidentas A. Brazauskas. Plenariniame posėdyje buvo išklausyti 2 pranešimai: Sietlo (JAV) universiteto prof. J.A. Wellneris nagrinėjo statistikos, o Romos universiteto Volteros matematikos centro prof. L. Accardis – kvantinės tikimybių teorijos problemas. Dirbta 6 sekcijose, perskaityta 216 216 pranešimų.
Nuotraukoje – grupė VI Tarptautinės Vilniuas tikimybių teorijos ir matematinės statistikos konferencijos dalyvių.
Instituto matematikai kviečiami ilgesniam ar trumpesniam laikui skaityti paskaitų ir dirbti mokslinio darbo į Vakarų Europos bei Amerikos universitetus ir mokslo centrus. Aleksandro von Humboldto stipendijas yra gavę habil. dr. V. Bentkus, daktarai K. Pileckas, L. Giraitis ir S. Jukna, kurie dirbo ar dirba Vokietijos universitetuose. Habil. dr. R. Mikulevičius dirba Pietų Kalifornijos universitete (JAV), habil. dr. A. Tempelmanas – Pensilvanijos universitete, habil..dr. D. Surgailis – kviečiamas į Klivlendo universitetą. Vien stambiausio pasaulinio tikimybininkų forumo – Tarptautinės tikimybių teorijos ir matematinės statistikos konferencijos rengimas Vilniuje reiškia pasaulinį Lietuvos tikimybių teorijos mokyklos pripažinimą.
Prisiminę I. Kanto mintį apie matematiką ne tokia griežta forma kaip jo paties, turime pripažinti, kad daugelio mokslų lygį lemia matematikos taikymas. Ypač dažnai matematikos prisireikia fizikos, technikos, ekonomikos mokslams, o jeigu turėsime galvoje ne vien matematikos mokslo kryptį, kurią straipsnyje apžvelgiau, o matematikos mokslų sritį, kuri be matematikos, apima informatiką, logiką, sistemotyrą ir statistiką, tai matematikos mokslų vaisiais naudojasi ir šiuolaikinės biologijos, medicinos, visuomenės ir kiti mokslai.
Savaime suprantama, kad kiekvienos srities specialistų rengimui didžiulę įtaką turi jos mokslo lygis ir turimų specialistų kvalifikacija.
Tad galvodami apie Lietuvos ateitį, jos intelektualinį potencialą, turime bet kuriomis (ir sunkiomis ekonominėmis šių dienų) sąlygomis puoselėti šią nedidelę, bet stiprią mokslo šaką, akad. J. Kubiliaus kadaise pavadintą „visų mokslų tarnaite“, – matematiką.
 Patekote į pirmąjį lietuvišką domeną.
Patekote į pirmąjį lietuvišką domeną. 





